Il y a deux cas possibles pour cette dernière difficulté, pour une question de parité qu'il est peu utile de développer ici, d'autant plus que j'en suis très probablement incapable. Sachez seulement que si, comme dans la combinaison suivante ou celle de l'étape précédente, on se limite aux mouvements qui conservent les deux faces carrées, on ne peut agir au final que sur un nombre de pièces multiple de 4 pour les faces du haut et du bas (étape 3 : deux coins et deux triangles de la face supérieure, ci-dessous : deux triangles sur chaque face). Dans la moitié des cas, on se retrouve dans des cas sympathiques, et pour le reste j'ai dû aller puiser dans l'impressionnante collection de formules de Jaap pour réussir à finir le square one à tous les coups (voir deuxième formule).

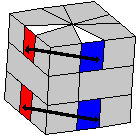
La première formule échange deux triangles adjacents sur chaque face, sans toucher à l'ordre des coins. Comme la face du bas est déjà finie, il est nécessaire d'effectuer cette formule un nombre pair de fois afin de ne pas détruire celle-ci. Typiquement, on réalise une permutation cyclique de trois triangles de la face blanche en effectuant une fois la combinaison, puis par exemple O3 ou Oi3, puis une nouvelle fois la combinaison, ce qui laisse la face verte intact au final. Observez l'image pour voir quels triangles sont concernés par la combinaison : Oi2-R-B3-R-Oi-Bi-L-Oi2-B-L

J'ai hésité à faire une page pour la dernière étape, qui ne pose en principe aucun problème si vous êtes arrivés jusqu'ici, mais comme chez.com offre un hébergement quasi illimité, vous pouvez vous rendre à la dernière étape par ici !